成电人物

　　研究生课程《现代数字信号处理理论与算法》在线开课两周了，效果还不错！信息与通信工程学院万群教授高兴地说，“开课前有心理压力，开课后尝到了甜头！”

　　这门课程面向的是学院2019级研究生。万群教授这学期带了一个教学班，上限人数是140人。正式上课后，发现在线课堂的“教室”里常常进来160多人。

　　显然，在线课堂为学生“蹭课”提供了极大的便利。而且，教学视频在线回放也可以在更大范围惠及更多的学生。对此，他的态度是：“欢迎感兴趣的同学都来蹭课！”

　　“这个课程对其他专业的学生也有借鉴作用！”他说，“我特别强调整体性思维，希望帮助更多学生把孤立的知识点联系起来，自己发现课程难点背后的直观而朴素的道理！”

充分准备：“以为很难，结果虚惊一场！”

　　万群教授以前没有上过在线课，当“主播”对他来说是人生第一次。刚开始接到“线上开学”的通知，他还是有点紧张，以为熟悉在线教学的工具和平台会比较复杂。

　　后来真正用起来，发现各个在线教学平台大同小异，并没有想象的那么难。但他依然不敢大意，生怕电脑或网络出现问题。

　　为了减小风险，他准备了两台电脑，上课的时候同时开机。一旦遇到问题，立即启用另一台电脑。手机上也装上了相应的程序。他说：“就怕出故障，所以必须留后招！”

　　开学前，他和助教一起约了2019级的研究生在线测试，反反复复测试很多次，把能考虑到的方面都考虑了，把在教学群里发现的共性问题都解决掉了。

　　他今年没有带本科生的课程，但主动加入了本科生的教学群。这是因为本科生要比研究生早一周开学，本科生遇到的问题都可以成为他的参考。

　　由于课程涉及信号处理的概念、定义和算法等诸多知识点，以前在教室里上课时，他都力求把这些知识点串起来，并随时引导学生讨论。现在线上授课，互动性相对受限。

　　因此，为了让学生更加容易接受课程内容，尤其是理解一些难点、重点，他把以前比较“浓缩”的PPT做了更多的分解，让学生明白一些公式、算法的推导过程。

　　从2004年开始上这门课程，他的PPT越讲越浓缩，引申的内容和知识点常在黑板上推演呈现；而这学期，他反其道行之，把浓缩的PPT又做得详细了起来。

　　他说：“这样做，都是为了让学生更容易接受！”

破冰之旅：专门用一个课时讲方法论

　　3月2日，星期二，这是万群教授本学期的第一节课，主要是概述课程基本情况。这门课是信号与信息处理等专业的核心专业基础课。

　　课程主要介绍信号处理的正交原理及其应用，包括功率谱密度估计、维纳滤波、卡尔曼滤波、空间谱估计等信号模型和处理算法。

　　考虑到学生的接受情况，他专门用了一个学时，特别介绍了学习这门课程的方法论。

　　什么是“现代数字信号处理理论与算法”？对这个概念的定义，仁者见仁、智者见智。万群参考了恩格斯对“共产主义”的定义，给出了自己的定义。

　　恩格斯说：“共产主义是关于无产阶级解放的条件的学说。”万群认为，“现代数字信号处理理论是关于数字信号处理算法适用的条件的学说。”

　　“我们要知道每一种算法的适用条件。”他强调说，“算法不同，条件就不同。如果用错地方，它也会水土不服。即便一种算法在这里表现很好，换个地方效果可能大打折扣。”

　　他提醒同学们，实际上，我们在具体的领域描述要解决的问题时，就要界定清楚具体条件。这是适用最佳算法的前提和基础。

　　怎么样清楚地界定具体条件呢？他告诉同学们三个秘诀：

　　第一是问题导向，即要明白一个算法到底是在算什么；

　　第二是目标导向，即明白算法的性能界限；

　　第三是需求导向，要考虑算法的成本、复杂度和稳健性等。

　　这样做的目的，就是要培养信号与信息处理相关专业研究生的创新能力和实践能力，促进研究生夯实本学科的基础理论功底，增强对学科发展前沿的了解。

整体思维：理解直观和简洁的朴素道理

　　万群教授特别强调“整体性思维”的重要性。他说，这门课程要启发学生掌握线性处理算法、均方误差准则、联合高斯分布之间内在的理论联系，从而将线性代数、矩阵理论与方法、信号与系统、概率统计、随机过程、凸最优化等信号与信息处理课程体系中的知识点转化成三种思维能力。

　　这三种思维能力分别是：从低维到高维的空间思维能力，从确定性到随机性的概率思维能力，从概念定义到问题导向的探究思维能力。

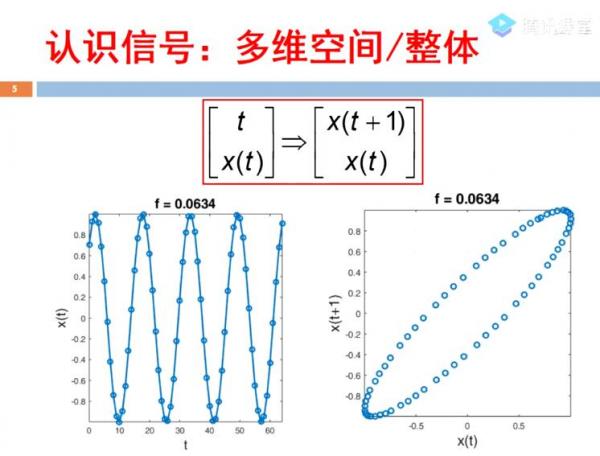
　　从低维到高维的空间思维方式，如启发学生建立长度/面积/体积/行列式、功率/方差/协方差矩阵、正弦波波形/线性自回归模型、最小方差无失真相应/维纳滤波/卡尔曼滤波（低维)之间的统一认识，从而吹散笼罩在行列式、协方差矩阵、信号复杂性、滤波（高维）等知识点上的迷雾。

　　从确定性到随机性的概率思维方式，如启发学生重新认识离散时间傅里叶变换、最小方差无失真相应、子空间分析等滤波算法及其背后优化准则的一致性（确定性），以及贝叶斯认识的局限性和费歇尔频率主义的差异（随机性）。

　　从概念定义到问题导向的探究思维方式，如以零门槛方式启发学生追溯高斯分布、拉普拉斯分布、均值、方差、离散时间傅里叶变换等基本概念、定义、算法背后统一的基础问题，从掌握单个知识点的能力转化为解决一类问题的能力。

　　有了这三种思维方法，万群教授可以轻松地用“勾股定理”通俗地解释“正交原理”，用“行列式”这一个概念来定义长度、面积、体积等三种不同的事物，并对应解释数据之间为什么存在“线性关系”。

　　他说：“虽然我校本科阶段已有先修课程《数字信号处理》，但学生对《数字信号处理》知识的掌握程度不同，并且本科课程与研究生课程在思维方式、工具水平上存在显著差异，所以，我再三强调要通过整体性思维揭开难点背后直观和简洁的朴素道理。” 

教学改革：三管齐下转变学生的思维

　　与三种思维能力相对应，他还提出了低维与高维相统一、确定性与随机性相统一、概念定义与背景问题相统一的教学方法。 

　　低维与高维相统一的教学方法，可突破信号波形呈现方式的局限和浅显层面的误导，将低维呈现的非线性卷绕在一起的复杂信号背后的高维线性结构呈现出来，有利于学生直观的抓住信号空时频变化规律和信号复杂性的本质特性。

　　确定性与随机性相统一的教学方法，有利于学生抓住确定性/随机性的匹配滤波、最小二乘/维纳滤波等信号处理算法以及高斯分布/拉普拉斯分布假设对应的优化准则的一致性，在一个统一的框架下明确课程中各种信号处理算法的最优性、潜在的假设条件及其适用范围，做一个有自信、负责任的算法分析者与设计者。

　　概念定义与背景问题相统一的教学方法，可激发学生的探究兴趣，一方面启发学生探究简单的信号处理算法背后一脉相承的深厚理论基础，另一方面启发学生探究复杂的信号处理算法背后简洁朴素的基本原理。

　　在具体的课程设计上，万群教授在平时成绩中增加了课堂讨论的分量，增加学生参与度，从而使学生在形成知识体系后，进一步拓宽知识面。他还通过建立学习小组、定期组织学习心得分享交流会等方式，来达到探究式教学方式和学生思维方式转变的目的。

　　据了解，2019年万群教授有五篇教研教改论文被IEEE TALE和第五届先进教育与管理国际会议录用，这些论文的第二作者都是2018级选修这门课程的研究生。

　　万群教授表示：“我希望2019级研究生也能在这个课程中受到启发，这对他们未来从事相关研究大有裨益！”