科研学术

　　近日，电子科技大学信息与通信工程学院博士生刘佳妮在朱策教授和刘翼鹏副教授的指导下以第一作者身份撰写的标题为Tensor Regression的综述性文章（187页）在机器学习领域著名期刊Foundations and Trends in Machine Learning发表。这一工作是2008年该期刊创刊14年来，中国学者首次以第一作者身份在这个期刊上发表的文章。

　　作为机器学习领域著名的期刊，Foundations and Trends in Machine Learning由机器学习领域著名专家Michael I. Jordan担任主编。期刊每年发表的文章不超过4篇，创刊14年共发表40余篇文章，其中多篇文章是主题方向的经典作品，单篇谷歌引用近万次；主要作者包括机器学习和相关领域著名资深专家Michael I. Jordan、 Yoshua Bengio、Bernhard Schölkopf、 Francis Bach、Stephen Boyd等。其每篇文章还被分配有国际标准书号（ISBN），作为专著出版。

　　《Tensor Regression》这个工作是行业第一篇针对张量回归分析理论、方法和应用的系统性综述。回归分析是机器学习、信号处理、数据挖掘、计算机视觉的核心技术之一。随着多维数据的涌现，传统的回归分析方法很难从复杂的数据结构中获取有用的信息。并且随之而来的庞大的计算和存储需求也是一个巨大的挑战。张量表示方式的引入，使传统的回归分析方式可以自然而然地扩展到高阶数据处理当中。低秩张量的表示不仅极大减少了回归模型所需的参数量，进而提高计算效率，而且尽可能保留了多维数据的结构信息。

　　这篇文章全面总结了张量回归的各种方法（如图1、图2所示）。从传统的回归分析方式讲起，追溯各类张量回归方法的起源，并分析讨论不同方法的优缺点，并对现有的应用方向及相关公开数据集（如图3所示）、公开软件库做了归纳整理。同时，通过图文结合的形式，以实例分析（如图4所示）力求让读者尽可能理解不同的线性和非线性张量回归在不同领域的应用，这也是本文的特色之一。读者可以通过这篇文章全面系统的了解如何利用张量分析技术解决各种多维数据相关的回归问题，以及现有的张量回归分析技术及其优缺点、各个应用领域及可以用来验证的公开数据集、公开软件库。

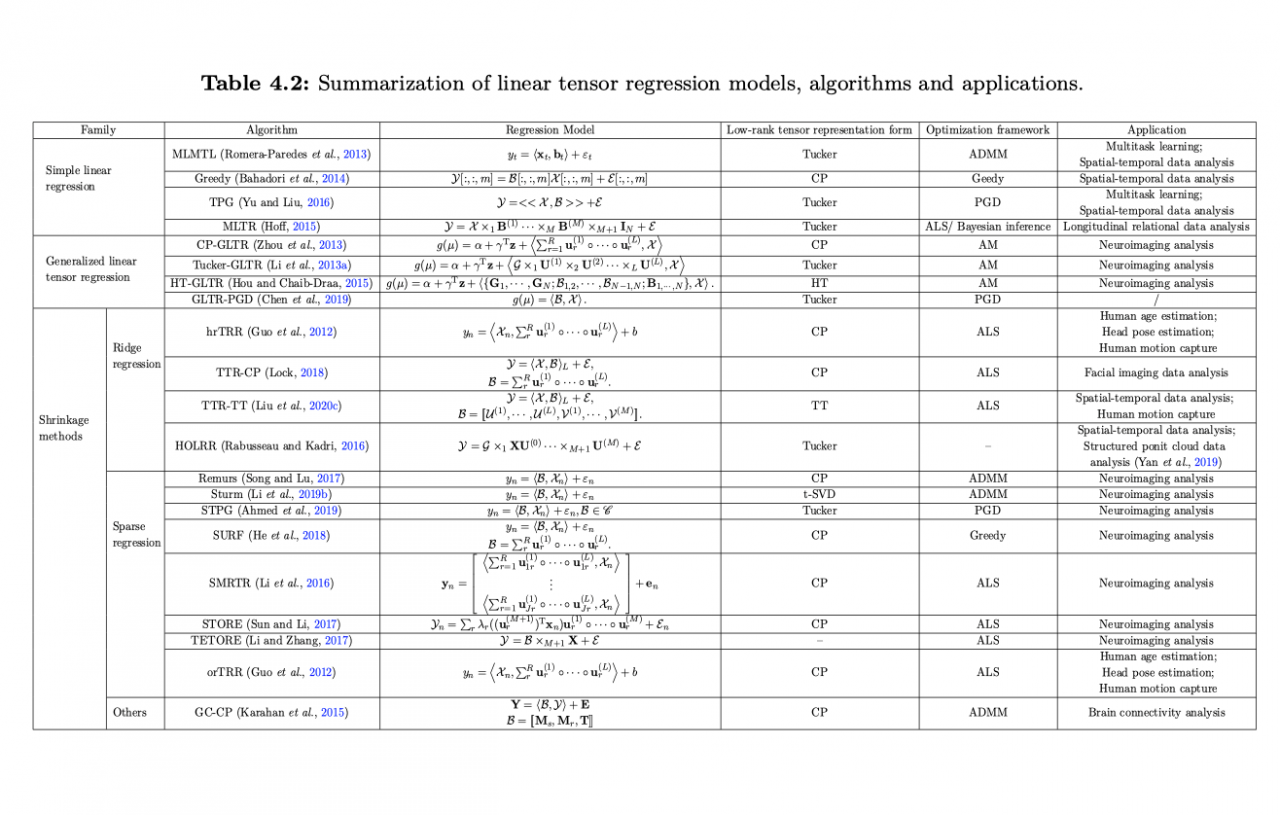
图1　线性张量回归模型、算法和应用总结

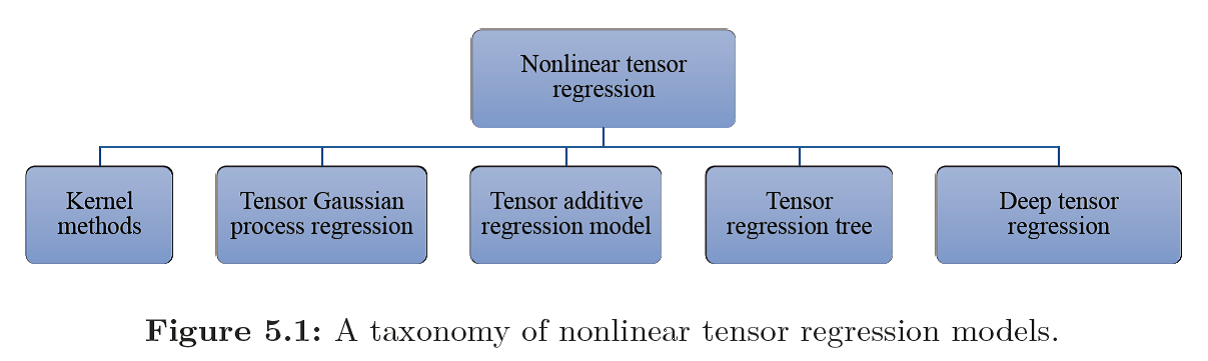
图2  主要非线性张量回归方法总结

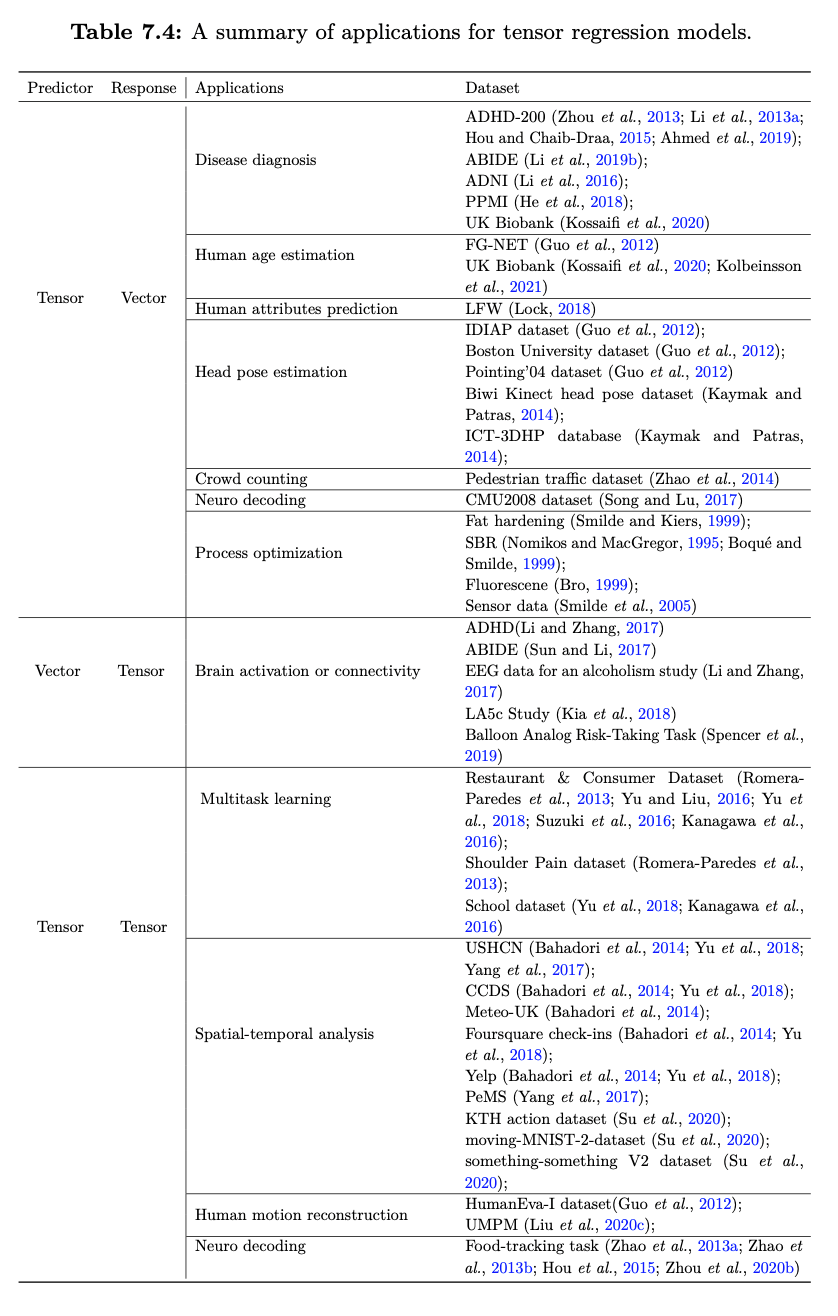
图3　张量回归模型应用总结

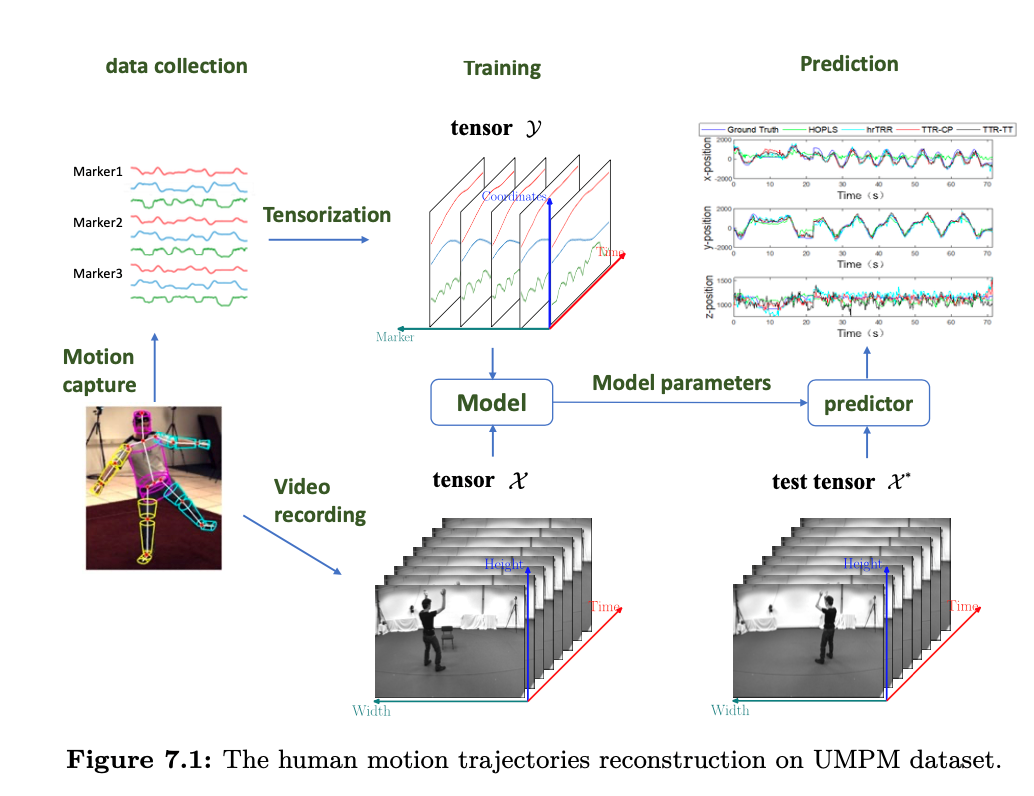
图4　人体行为轨迹重建

　　作为期刊文章被分配完整的期号、刊号和页码等的同时，《Tensor Regression》也被Now Publishers作为英文专著出版。全书正文共187页，包含10个表，32张图；电子版国际标准书号为：978-1-68083-887-9，纸质版国际标准书号为：978-1-68083-886-2。

　　刘佳妮在朱策教授和刘翼鹏副教授的指导下，主要从事张量回归分析相关理论、方法与应用工作。以张量计算为基础，重点研究多维数据相关的回归方法，主要应用在多维图像或视频分析、社交数据分析等。她已发表张量数据分析相关的期刊论文8篇，其合著的书籍《Tensor Computation for Data Analysis》于2021年9月由施普林格（Springer）出版。目前她在鲁汶大学（比利时）电子工程系进行联合培养，合作导师Johan A. K. Suykens教授是机器学习领域著名专家，最小二乘支持向量机（LS-SVM）的提出者，IEEE Fellow，WCCI 2020、ICASSP 2016等行业旗舰会议的主旨报告专家。

　　这项工作的另一名博士生作者龙珍在朱策教授和刘翼鹏副教授的指导下主要从事低秩张量表示、张量补全相关理论、方法与应用工作，已发表低秩张量方向期刊论文7篇，其中ESI高被引论文2篇，合作专著2本。她目前在格勒诺布尔大学（法国）gipsa-lab进行联合培养，合作导师Pierre Comon教授是信号处理领域著名专家，独立成分分析（ICA）的主要提出者，SIAM Fellow、IEEE Fellow、EURASIP Fellow，法国科学院Monpetit奖和IMT大奖获得者。

　　相关链接：

　　1.文章引用格式：Jiani Liu, Ce Zhu, Zhen Long and Yipeng Liu, "Tensor Regression", Foundations and Trends® in Machine Learning, vol. 14, no. 4, pp 379-565, 2021.

　　2.《Tensor Regression》的获取链接：

https://www.nowpublishers.com/article/Details/MAL-087

　　3.《Tensor Computation for Data Analysis》的获取链接：https://www.springer.com/cn/book/9783030743857